Расчет дисперсии в Excel: Руководство с примерами
Дисперсия — это статистическая мера, которая показывает, насколько набор чисел разбросан. Это ключевое понятие в финансах, науке и многих других областях, помогающее нам понять изменчивость или разброс данных. Excel предоставляет простой способ вычисления дисперсии, что делает его доступным как для начинающих, так и для продвинутых пользователей. В этой статье мы рассмотрим, как это сделать с помощью четких примеров.
Что такое дисперсия?
Введение в функции дисперсии Excel
Как рассчитать дисперсию в Excel?
- VAR.S vs VAR.P – Расчет дисперсии по выборке или генеральной совокупности
- VAR.S vs VARA – Расчет дисперсии с учетом или без учета текста и логических значений
Дисперсия vs Стандартное отклонение
Что такое дисперсия?
Дисперсия — это статистический термин, который описывает степень, в которой числа в наборе данных отличаются от среднего значения или усредненного значения этих чисел. По сути, она измеряет, насколько числа разбросаны. Важный момент в понимании дисперсии заключается в том, что она количественно определяет степень вариации или разброса внутри набора значений. Высокая дисперсия указывает на то, что числа сильно разбросаны; низкая дисперсия предполагает, что они плотно сконцентрированы вокруг среднего значения.
Простой пример для иллюстрации дисперсии:
Сценарий: Рассмотрим класс из пяти студентов и их результаты на математическом тесте из 100 баллов. Оценки составляют 90, 92, 88, 91 и 89.
Расчет среднего значения: Сначала находим среднее значение (среднюю) оценку. Среднее значение равно
Расчет дисперсии: Затем мы рассчитываем дисперсию. Это включает вычитание среднего значения из каждой оценки, возведение результата в квадрат и последующее усреднение этих квадратичных разностей.
= [0 + 4 + 4 + 1 + 1] / 5
= 10 / 5
= 2
На диаграмме показано распределение оценок:
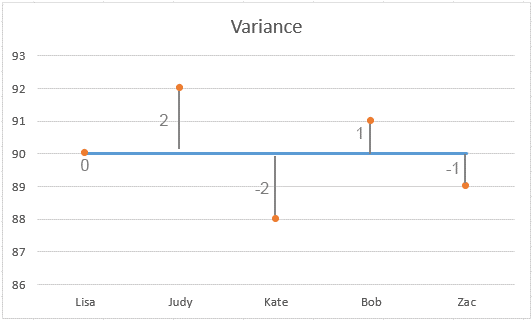
Понимание результата:
Низкая дисперсия: В этом примере дисперсия равна 2. Это относительно низкое значение, указывающее на то, что большинство оценок близки к среднему значению (90). Чем ниже дисперсия, тем ближе индивидуальные числа в наборе к среднему значению.
Нулевая дисперсия: Если бы все студенты получили точно 90 баллов, дисперсия была бы равна 0, что указывало бы на полное отсутствие изменчивости. Каждая оценка была бы одинаковой.
Высокая дисперсия: Напротив, более высокая дисперсия указывала бы на то, что оценки больше разбросаны относительно среднего значения, демонстрируя большую изменчивость в успеваемости студентов.
Подводя итог, дисперсия дает нам числовое значение, которое помогает количественно оценить, насколько оценки (или любой набор чисел) отклоняются от среднего значения, предоставляя представление о согласованности или изменчивости данных.
Введение в функции дисперсии Excel
Excel предоставляет несколько функций для расчета дисперсии, каждая из которых предназначена для различных сценариев работы с данными.
Понимание этих функций имеет решающее значение для точного статистического анализа.
VAR.S (Выборочная дисперсия, только числа):
- Вычисляет дисперсию на основе выборки генеральной совокупности.
- Лучше всего используется при анализе подмножества данных для вывода о целом.
VAR.P (Генеральная дисперсия, только числа):
- Вычисляет дисперсию для всей генеральной совокупности.
- Идеально подходит, когда у вас есть полные данные, а не только выборка.
VARA (Выборочная дисперсия, включая текст и логические значения):
- Аналогична VAR.S, но включает текст и логические значения в расчет (текст считается как 0, ИСТИНА как 1, ЛОЖЬ как 0).
- Полезна, когда ваш набор данных содержит смешанные типы (числа, текст и логические значения).
VARPA (Генеральная дисперсия, включая текст и логические значения):
- Версия генеральной дисперсии для VARA.
- Включает все типы данных в расчете дисперсии для всей генеральной совокупности.
VAR (Устаревшая выборочная дисперсия):
- Старая версия VAR.S, в основном используемая в Excel 2007 и более ранних версиях.
- Рекомендуется использовать VAR.S в новых версиях для обеспечения согласованности и ясности.
VARP (Устаревшая генеральная дисперсия):
- Старая версия VAR.P.
- Как и VAR, рекомендуется использовать VAR.P в новых версиях Excel.
Различия и сравнения:
- Выборка vs Генеральная совокупность: VAR.S и VARA предназначены для выборок, тогда как VAR.P и VARPA предназначены для всей генеральной совокупности.
- Учет типа данных: VARA и VARPA включают текст и логические значения в расчет, в отличие от VAR.S и VAR.P.
- Устаревшие vs Современные функции: VAR и VARP являются старыми функциями и могут быть заменены на VAR.S и VAR.P для лучшей совместимости с текущими версиями Excel.
Таблица сравнения:
| Функция | Учитываемый тип данных | Генеральная совокупность или выборка | Случай использования |
| VAR.S | Только числа | Выборка | Выборочная дисперсия для числовых данных |
| VAR.P | Только числа | Генеральная совокупность | Генеральная дисперсия для чисел |
| VARA | Числа, текст, логические значения | Выборка | Выборочная дисперсия для смешанных данных |
| VARPA | Числа, текст, логические значения | Генеральная совокупность | Генеральная дисперсия для смешанных данных |
| VAR | Только числа | Выборка | Устаревшая функция для выборочной дисперсии |
| VARP | Только числа | Генеральная совокупность | Устаревшая функция для популярной |

Раскройте магию Excel с Kutools AI
- Умное выполнение: Выполняйте операции с ячейками, анализируйте данные и создавайте диаграммы — всё это посредством простых команд.
- Пользовательские формулы: Создавайте индивидуальные формулы для оптимизации ваших рабочих процессов.
- Кодирование VBA: Пишите и внедряйте код VBA без особых усилий.
- Интерпретация формул: Легко разбирайтесь в сложных формулах.
- Перевод текста: Преодолейте языковые барьеры в ваших таблицах.
Как рассчитать дисперсию в Excel?
В этом разделе мы приведем два примера, чтобы продемонстрировать, как рассчитать дисперсию в Excel, и объясним различия между различными функциями дисперсии. В результате вы увидите, что различные функции дисперсии дают совершенно разные результаты для одних и тех же примеров данных.
VAR.S vs VAR.P – Расчет дисперсии по выборке или генеральной совокупности
Сценарий: Расчет дисперсии для небольшой выборки генеральной совокупности vs всей генеральной совокупности.
Пример: Рассчитайте дисперсию для значений в столбце A2:A12.
Формула: Выберите пустую ячейку и введите одну из следующих формул по необходимости, затем нажмите клавишу Enter.
Получение дисперсий для выборки большого набора данных (предполагая, что значения в A2:A12 являются частью большого набора данных)
=VAR.S(A2:A12)
Получение дисперсии для всей генеральной совокупности (предполагая, что значения в A2:A12 представляют собой весь набор данных)
=VAR.P(A2:A12)
Как видите, одни и те же значения, но использование разных функций дисперсии даст разные результаты.
Почему результаты VAR.S и VAR.P различны?
- VAR.S: Эта функция используется, когда ваш набор данных представляет собой выборку из большей генеральной совокупности. Она вычисляет дисперсию на основе метода «n-1», где «n» — это количество точек данных в выборке. Использование «n-1» вместо «n» в качестве знаменателя корректирует смещение в выборке, делая ее несмещенной оценкой дисперсии генеральной совокупности. Она предоставляет оценку того, как данные в выборке меняются вокруг среднего значения выборки.
- VAR.P: Эта функция используется, когда ваш набор данных представляет собой всю генеральную совокупность, а не только выборку из нее. Она вычисляет дисперсию на основе метода «n», где «n» — это количество точек данных в генеральной совокупности. Она предполагает, что набор данных охватывает всю генеральную совокупность, поэтому нет необходимости корректировать смещение, как в VAR.S.
- Подводя итог, основное различие заключается в знаменателе формулы. VAR.S использует «n-1» для учета выборочного характера данных, тогда как VAR.P использует «n» для данных генеральной совокупности, где нет выборки. В зависимости от вашего набора данных и того, является ли он выборкой или полной генеральной совокупностью, вы должны выбрать соответствующую функцию для расчета дисперсии.
VAR.S vs VARA – Расчет дисперсии с учетом или без учета текста и логических значений
Сценарий: Принятие решения о включении логических значений и текста в расчет дисперсии.
Пример: Рассчитайте дисперсию для значений в столбце A2:A12.
Формула: Выберите пустую ячейку и введите одну из следующих формул по необходимости, затем нажмите клавишу Enter.
Получение дисперсий для выборки большого набора данных, игнорируя текст и логические значения.
=VAR.S(A2:A12)
Получение дисперсии для выборки большого набора данных, включая текст и логические значения.
=VARA(A2:A12)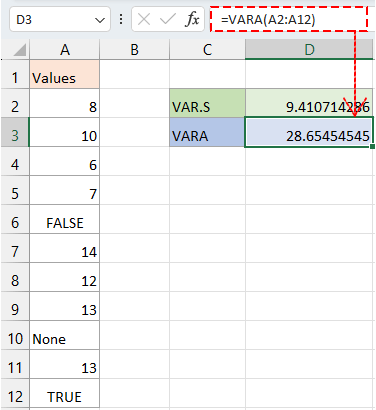
Ускорьте расчеты времени и даты
Kutools for Excel's Date Time Helper — невероятно эффективный инструмент, созданный для упрощения сложных расчетов времени и даты. Попробуйте его и убедитесь, как он преобразит ваш опыт управления данными!
Дисперсия vs Стандартное отклонение
Сходства:
Мера разброса:
И дисперсия, и стандартное отклонение являются статистическими мерами, используемыми для описания разброса или дисперсии внутри набора данных. Они количественно определяют, насколько далеко отдельные числа в наборе отклоняются от среднего значения (средней величины).
Анализ данных:
Оба широко используются в статистическом анализе для понимания изменчивости данных. Они необходимы в таких областях, как финансы, исследования, контроль качества и другие.
Расчет на основе среднего значения:
Расчет как дисперсии, так и стандартного отклонения начинается со среднего значения набора данных. Они оценивают изменчивость в отношении этого центрального значения.
Различия:
Единицы измерения:
Дисперсия: Квадратные единицы исходных данных. Например, если данные указаны в метрах, дисперсия будет в квадратных метрах.
Стандартное отклонение: Те же единицы, что и исходные данные. Продолжая пример, если данные указаны в метрах, стандартное отклонение также будет в метрах.
Интерпретация:
Дисперсия: Предоставляет квадратичную оценку, которая может быть менее интуитивно понятной для интерпретации, поскольку она не находится в том же масштабе, что и исходные данные.
Стандартное отклонение: Более интерпретируемо, поскольку оно находится в тех же единицах, что и данные. Оно указывает среднее расстояние точек данных от среднего значения.
Математическое определение:
Дисперсия: Среднее значение квадратов разностей от среднего значения.
Стандартное отклонение: Квадратный корень из дисперсии.
Чувствительность к экстремальным значениям:
Дисперсия: Более чувствительна к выбросам, поскольку возводит разности в квадрат.
Стандартное отклонение: Хотя и подвержено влиянию выбросов, оно менее чувствительно по сравнению с дисперсией из-за квадратного корня.
Применения:
Дисперсия:
Используется, когда акцент сделан на квадратичной величине дисперсии.
Полезна в статистических моделях и вычислениях, где возведение в квадрат необходимо для нейтрализации отрицательных значений.
Часто используется в финансовых моделях для оценки рисков, поскольку измеряет волатильность.
Стандартное отклонение:
Чаще используется в отчетах и повседневных приложениях благодаря своей прямой связи с масштабом данных.
Необходимо в эмпирических исследованиях для понимания изменчивости.
Часто используется в контроле качества, прогнозах погоды и стандартных баллах тестов.
Заключение:
Хотя дисперсия и стандартное отклонение оба служат для измерения разброса набора данных, их применения различаются из-за их единиц измерения и интерпретируемости. Стандартное отклонение, благодаря своей прямой связи с масштабом данных, обычно более удобно для пользователя, особенно в практических, повседневных контекстах. Дисперсия, с другой стороны, чаще подходит для математических и статистических моделей.
Этот обзор и сравнение должны предоставить четкое понимание того, когда и почему использовать каждую функцию дисперсии в Excel, позволяя проводить более точный и содержательный анализ данных. Для получения дополнительных стратегий работы с Excel, которые могут повысить вашу управляемость данными, узнайте больше здесь..
Лучшие инструменты для повышения производительности Office
Kutools для Excel - Помогает вам выделиться из толпы
| 🤖 | KUTOOLS AI Помощник: Революционизируйте анализ данных на основе: Интеллектуальное выполнение | Генерация кода | Создание пользовательских формул | Анализ данных и создание диаграмм | Вызов функций Kutools… |
| Популярные функции: Поиск, Выделение или Отметка дубликатов | Удалить пустые строки | Объединить столбцы или ячейки без потери данных | Округлить без формулы ... | |
| Супер VLookup: Множественные критерии | Множественные значения | На нескольких листах | Распознавание нечетких соответствий... | |
| Расширенный раскрывающийся список: Простой раскрывающийся список | Зависимый раскрывающийся список | Раскрывающийся список с множественным выбором... | |
| Управление столбцами: Добавить определенное количество столбцов | Переместить столбцы | Переключить статус видимости скрытых столбцов | Сравнить столбцы для выбора одинаковых и разных ячеек ... | |
| Основные функции: Сетка фокусировки | Дизайн листа | Улучшенная строка формул | Управление книгами и листами | Библиотека автотекста (Авто текст) | Выбор даты | Объединить данные | Шифрование/Расшифровка ячеек | Отправка писем по списку | Супер фильтр | Специальный фильтр (фильтр жирного/курсивного/зачеркнутого текста...) ... | |
| Топ-15 наборов инструментов: 12 инструментов для работы с текстом (Добавить текст, Удалить определенные символы ...) | 50+ типов диаграмм (Диаграмма Ганта ...) | 40+ практических формул (Расчет возраста на основе даты рождения ...) | 19 инструментов вставки (Вставить QR-код, Вставить изображение по пути ...) | 12 инструментов преобразования (Преобразовать в слова, Конвертация валюты ...) | 7 инструментов объединения и разделения (Расширенное объединение строк, Разделить ячейки Excel ...) | ... и многое другое |
Kutools для Excel имеет более 300 функций, гарантируя, что то, что вам нужно, находится всего в одном клике...
Office Tab - Включите работу с вкладками в Microsoft Office (включая Excel)
- Один щелчок, чтобы переключаться между десятками открытых документов!
- Сократите сотни кликов мышью каждый день, попрощайтесь с болью в руке от мыши.
- Повышает вашу продуктивность на 50% при просмотре и редактировании нескольких документов.
- Добавляет эффективные вкладки в Office (включая Excel), как в Chrome, Edge и Firefox.
Содержание
- Что такое дисперсия?
- Введение в функции дисперсии Excel
- Как рассчитать дисперсию в Excel?
- VAR.S vs VAR.P – Расчет дисперсии по выборке или генеральной совокупности
- VAR.S vs VARA – Расчет дисперсии с учетом или без учета текста и логических значений
- Дисперсия vs Стандартное отклонение
- Связанные статьи
- Лучшие инструменты для повышения производительности офиса
- Комментарии